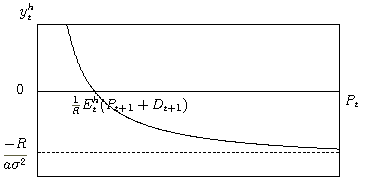
Figure 6.1: Demand function of the mean-variance utility maximizing belief

6.3.2  Non-utility-maximizing beliefs: technical traders

In subsection 6.3.1 we have derived the demand function for the risky asset under the assumptions that agents make price predictions and maximize a constant relative risk aversion utility function on a capital allocation line. However, if investors use technical trading rules, then they often do not try to make a point forecast of the price directly, but they make an investment decision based on the direction of a trend in prices. Pring (1992) defines technical analysis as the art of detecting a price trend in an early stage and maintaining a market position until there is enough weight of evidence that the trend has reversed. Thus, if we want to model technical traders, then we must define a demand function for the risky asset in another way as we did in section 6.3.1.

We take as an example the exponential moving-average trading rule. The advantage of this rule over the usual equally weighted moving-average trading rule is that it keeps the dimension of our model low. Demand functions for other technical trading rules can be derived according to the same concept. The exponential moving average at time t is equal to

MAt=µ Pt + (1-µ) MAt-1=µ
t-1
∑
j=0
(1-µ)j Pt-j + (1-µ)t MA0,     (25)
where 0 < µ < 1. In this formula more recent prices get a higher weight than prices further into the past. The advantage of moving-average rules is that they follow the trend, are easy to compute and smooth an otherwise volatile series. The smaller µ, the more the moving average smoothes the price series, or stated differently, the more the moving average follows the price series at a distance. A small µ places little weight on current price and can be used to detect long term trends, while a large µ places large weight on current price and can be used to detect short term trends.
247